Geometry Unit 10 Circles Quiz 10-3 Answers empowers students with a comprehensive understanding of circles, equipping them to tackle geometry challenges with precision and confidence. This meticulously crafted guide unveils the fundamental concepts of circles, their properties, and practical applications, ensuring a thorough grasp of this essential geometric shape.
Delving into the intricacies of circles, this guide explores the relationship between radius, diameter, and circumference, providing a solid foundation for solving circle-related problems. With step-by-step explanations and illustrative examples, students will master the formulas for calculating area and circumference, gaining proficiency in circle measurements.
Circle Concepts
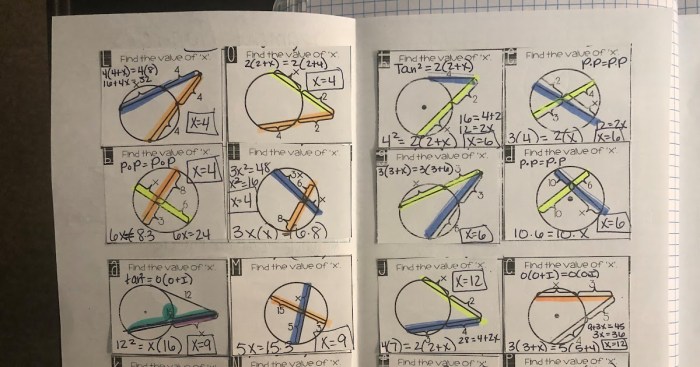
A circle is a plane figure that consists of all points equidistant from a given point, called the center. Circles have several important properties:
- The distance from the center to any point on the circle is called the radius.
- The diameter of a circle is the distance across the circle through the center, which is twice the radius.
- The circumference of a circle is the distance around the circle, which is equal to π times the diameter.
Circles are found in many real-world applications, such as:
- Wheels
- Gears
- Pulleys
- Clocks
- Architectural domes
Area and Circumference Calculations: Geometry Unit 10 Circles Quiz 10-3 Answers
The area of a circle is given by the formula:
A = πr²
where r is the radius of the circle.
The circumference of a circle is given by the formula:
C = 2πr
where r is the radius of the circle.
Here is a table summarizing the formulas for calculating the area and circumference of a circle:
| Formula | Description |
|---|---|
| A = πr² | Area of a circle |
| C = 2πr | Circumference of a circle |
Tangents and Secants
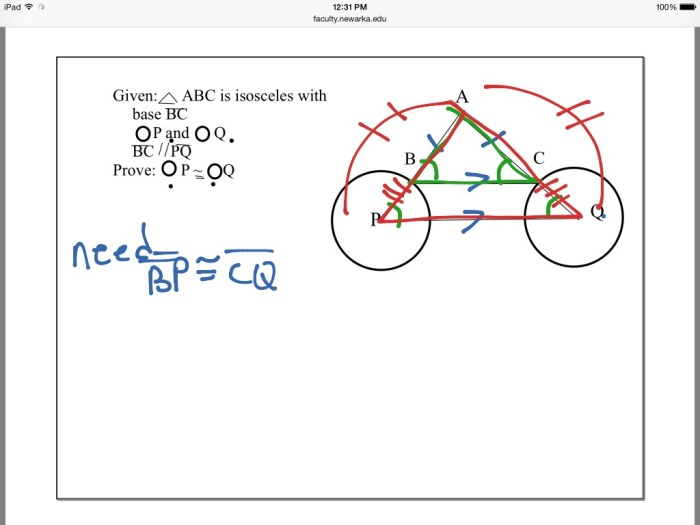
A tangent to a circle is a line that intersects the circle at exactly one point. A secant to a circle is a line that intersects the circle at two points.
The following properties and relationships hold for tangents and secants:
- The tangent to a circle at a point is perpendicular to the radius drawn to that point.
- The length of the tangent segment from the point of tangency to the point of intersection with a secant is equal to the radius of the circle.
- The product of the lengths of the two segments of a secant that intersects the circle outside the circle is equal to the square of the tangent segment.
Inscribed and Circumscribed Circles
An inscribed circle is a circle that is tangent to all sides of a polygon. A circumscribed circle is a circle that passes through all the vertices of a polygon.
The following properties and relationships hold for inscribed and circumscribed circles:
- The center of an inscribed circle is the point of intersection of the perpendicular bisectors of the sides of the polygon.
- The radius of an inscribed circle is equal to the distance from the center of the circle to any side of the polygon.
- The center of a circumscribed circle is the point of intersection of the perpendicular bisectors of the diagonals of the polygon.
- The radius of a circumscribed circle is equal to the distance from the center of the circle to any vertex of the polygon.
Applications in Geometry

Circles are used in a variety of applications in geometry, including:
- Finding the area and circumference of circles
- Constructing inscribed and circumscribed circles for polygons
- Solving geometric problems involving circles
- Applying the properties of circles to solve real-world problems
Circles are also used in a variety of fields outside of geometry, such as:
- Engineering
- Architecture
- Design
- Astronomy
- Physics
Common Queries
What is the formula for calculating the area of a circle?
A = πr², where r is the radius of the circle.
How do I find the circumference of a circle?
C = 2πr, where r is the radius of the circle.
What is the relationship between the radius, diameter, and circumference of a circle?
Diameter = 2 × Radius, Circumference = π × Diameter.