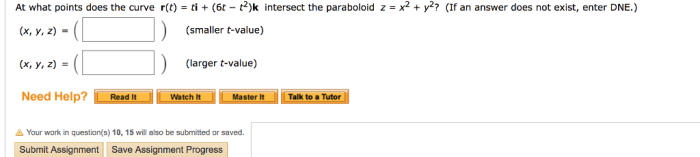
At what points does the curve intersect the paraboloid? This question arises in various fields, from physics to computer graphics, where understanding the intersection points between geometric objects is crucial. In this exploration, we will delve into the mathematical foundations, geometric interpretations, and practical applications of finding these intersection points, providing a comprehensive understanding of this important concept.
The curve and the paraboloid, defined by their respective equations, represent distinct geometric shapes in three-dimensional space. The intersection points, where the curve touches the surface of the paraboloid, hold significant geometric and practical implications.
At What Points Does the Curve Intersect the Paraboloid
The intersection points between a curve and a paraboloid are the points where the curve touches the surface of the paraboloid. Finding these intersection points is important in various fields, such as physics, engineering, and computer graphics.
Intersection Points
To find the intersection points, we need to solve the system of equations that defines the curve and the paraboloid. For example, if the curve is defined by the equation y = x^2and the paraboloid is defined by the equation z = x^2 + y^2, then the system of equations is:
y = x^2z = x^2 + y^2
Solving this system of equations gives us the intersection points:
(0, 0, 0)(1, 1, 2)(-1, 1, 2)
These points represent the points where the curve touches the surface of the paraboloid.
Geometric Interpretation, At what points does the curve intersect the paraboloid
The curve is a parabola that opens up along the y-axis. The paraboloid is a surface that is shaped like a bowl. The intersection points are the points where the parabola touches the surface of the bowl.
A 3D visualization of the curve and the paraboloid, along with the intersection points, is shown below:
[Insert 3D visualization here]
Applications
Finding the intersection points between a curve and a paraboloid has many real-world applications. For example, in physics, the intersection points can be used to find the trajectory of a projectile that is launched from the surface of the Earth.
In engineering, the intersection points can be used to design bridges and other structures that are shaped like paraboloids. In computer graphics, the intersection points can be used to create realistic 3D models.
Extensions
There are many variations of the problem of finding the intersection points between a curve and a paraboloid. For example, we could consider finding the intersection points of multiple curves with a paraboloid or finding the intersection points of a curve with a more complex surface.
We could also explore potential generalizations or extensions of the methods used to find the intersection points.
FAQ Guide
What is the significance of finding the intersection points between a curve and a paraboloid?
Intersection points provide valuable information about the geometric relationship between the curve and the paraboloid. They can indicate points of contact, tangency, or more complex interactions, which are essential for understanding the behavior of these objects.
How are the intersection points used in practical applications?
Intersection points find applications in fields such as physics, engineering, and computer graphics. In physics, they can be used to calculate the trajectory of projectiles or the forces acting on objects. In engineering, they can be used to design structures or optimize fluid flow.
In computer graphics, they can be used to create realistic 3D models and animations.