Unit 2 Linear Functions Homework Answers: A Comprehensive Guide to Success sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. Embark on an educational journey where the intricacies of linear functions unravel, empowering you with the knowledge and skills to conquer any homework challenge that comes your way.
Delving into the depths of this guide, you will encounter a comprehensive exploration of linear functions, their properties, and their applications. Prepare to master the art of graphing linear functions, solving linear equations, and utilizing these functions to model real-world phenomena.
With each concept explained with precision and clarity, you will gain a profound understanding that will serve as a solid foundation for your future academic endeavors.
Unit 2 Linear Functions Homework Overview: Unit 2 Linear Functions Homework Answers
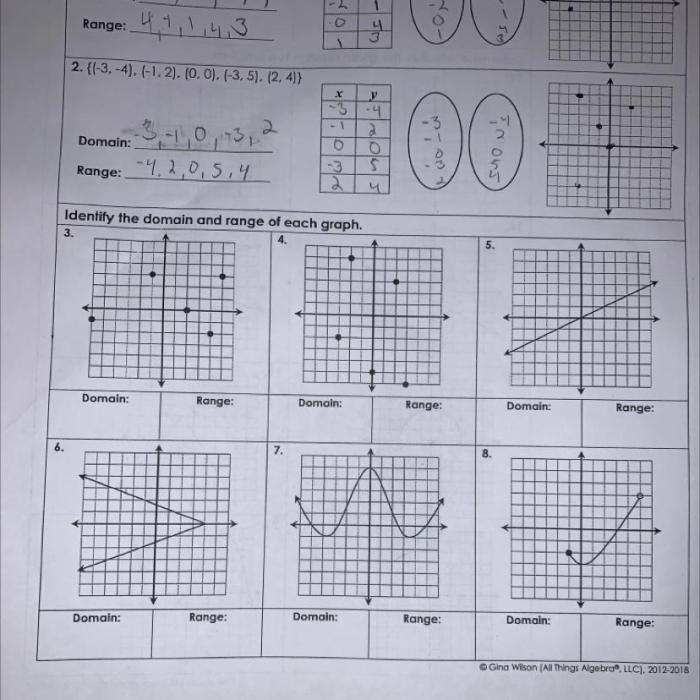
This homework assignment provides practice with the concepts and skills covered in Unit 2: Linear Functions. It reinforces the understanding of linear equations, graphing, and applications. The homework aims to assess students’ comprehension and ability to apply these concepts to solve problems.
Key Concepts and Skills
- Linear functions
- Slope and y-intercept
- Graphing linear functions
- Solving linear equations
- Applications of linear functions
Purpose and Objectives
- To reinforce understanding of linear functions.
- To develop skills in graphing and solving linear equations.
- To apply linear functions to real-world situations.
- To prepare students for future lessons on more advanced topics.
Linear Functions: Definitions and Properties

Linear functions are a fundamental concept in algebra. They are characterized by a constant rate of change, which is represented by the slope of the line. The y-intercept of a linear function is the point where the line crosses the y-axis.
Definition
A linear function is a function whose graph is a straight line. The equation of a linear function can be written in the form y = mx + b, where m is the slope and b is the y-intercept.
Properties
- The slope of a linear function is constant.
- The y-intercept of a linear function is the point where the line crosses the y-axis.
- Linear functions can be used to model a wide variety of real-world phenomena.
Examples
- The function f(x) = 2x + 1 is a linear function with a slope of 2 and a y-intercept of 1.
- The function g(x) = -3x + 5 is a linear function with a slope of -3 and a y-intercept of 5.
Graphing Linear Functions

Graphing linear functions is a useful skill that can be used to visualize the relationship between the input and output values of the function. The graph of a linear function is a straight line, and the slope and y-intercept of the line can be used to determine the equation of the function.
Steps for Graphing Linear Functions, Unit 2 linear functions homework answers
- Find the slope and y-intercept of the function.
- Plot the y-intercept on the y-axis.
- Use the slope to find another point on the line.
- Draw a straight line through the two points.
Importance of Slope and Y-Intercept
The slope of a linear function is important because it tells you the rate of change of the function. The y-intercept is important because it tells you the value of the function when the input value is 0.
Examples
- The graph of the function f(x) = 2x + 1 is a straight line with a slope of 2 and a y-intercept of 1.
- The graph of the function g(x) = -3x + 5 is a straight line with a slope of -3 and a y-intercept of 5.
Popular Questions
What is the purpose of this guide?
This guide aims to provide comprehensive support for students working on Unit 2 Linear Functions homework assignments. It offers clear explanations, step-by-step instructions, and practice exercises to enhance understanding and ensure success.
What key concepts are covered in this guide?
This guide covers essential concepts related to linear functions, including their definition, properties, graphing techniques, solving linear equations, and applications in various fields.
How can I use this guide effectively?
To maximize the benefits of this guide, it is recommended to read through the material carefully, work through the practice exercises, and seek clarification on any concepts that require further understanding. Consistency and dedication are key to achieving optimal results.