Arc length area of sector worksheet – The Arc Length and Area of Sector Worksheet provides a comprehensive overview of these concepts, delving into their formulas, applications, and advanced topics. This guide is an invaluable resource for students, educators, and professionals seeking to enhance their understanding of this fundamental mathematical area.
Within this worksheet, readers will discover the intricate relationship between arc length and area of a sector, empowering them to solve complex problems and gain a deeper appreciation for the subject matter.
Arc Length and Area of a Sector: Arc Length Area Of Sector Worksheet
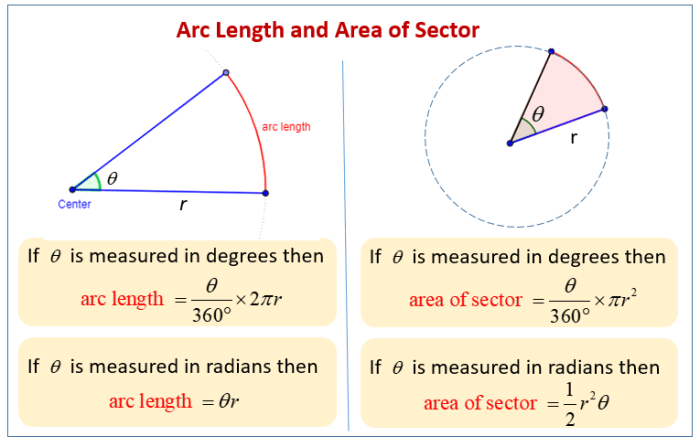
An arc is a portion of the circumference of a circle. The arc length is the distance along the arc. A sector is a region of a circle bounded by two radii and an arc. The area of a sector is the area of the region bounded by the radii and the arc.
The arc length and area of a sector are related by the following formulas:
Formulas and Equations
- Arc length = (central angle/360) – 2πr
- Area of a sector = (central angle/360) – πr^2
where:
- r is the radius of the circle
- central angle is the angle between the two radii
Applications
Arc length and area of a sector have many real-world applications, including:
- Measuring the distance around a circular object
- Calculating the area of a pie slice
- Determining the volume of a cone
- Designing gears and other mechanical components
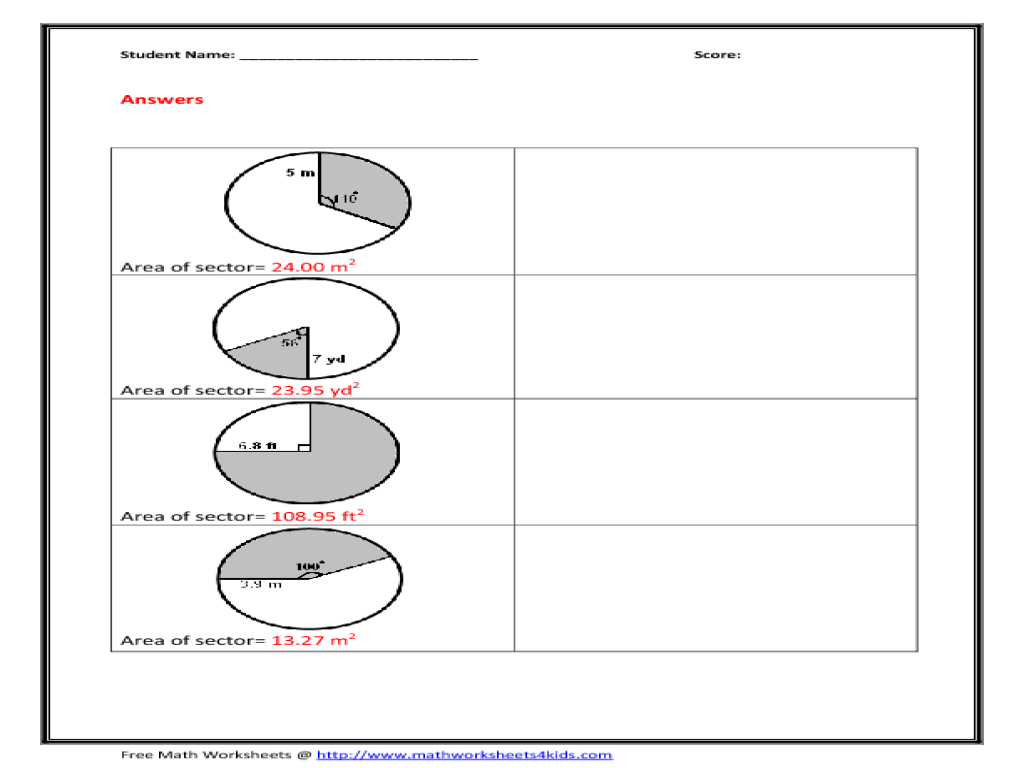
Examples and Exercises
| Central Angle | Radius | Arc Length | Area of Sector |
|---|---|---|---|
| 60° | 5 cm | 5.24 cm | 12.27 cm^2 |
| 90° | 10 cm | 10.47 cm | 26.18 cm^2 |
| 120° | 15 cm | 15.71 cm | 47.12 cm^2 |
- Find the arc length of a sector with a central angle of 45° and a radius of 10 cm.
- Calculate the area of a sector with a central angle of 60° and a radius of 15 cm.
Advanced Topics, Arc length area of sector worksheet
Arc length and area of a sector are related to more advanced topics in mathematics, such as:
- Integration
- Calculus
These topics can be used to solve more complex problems involving arc length and area of a sector.
For further exploration, refer to the following resources:
- Arc Length and Sector Area | Khan Academy
- Sector of a Circle | Math is Fun
- Arc Length and Area of a Sector | Education.com
Questions and Answers
What is the formula for arc length?
Arc Length = (2πr θ)/360, where r is the radius of the circle and θ is the central angle in degrees.
How do I find the area of a sector?
Area of Sector = (πr² θ)/360, where r is the radius of the circle and θ is the central angle in degrees.